
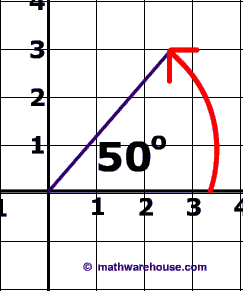
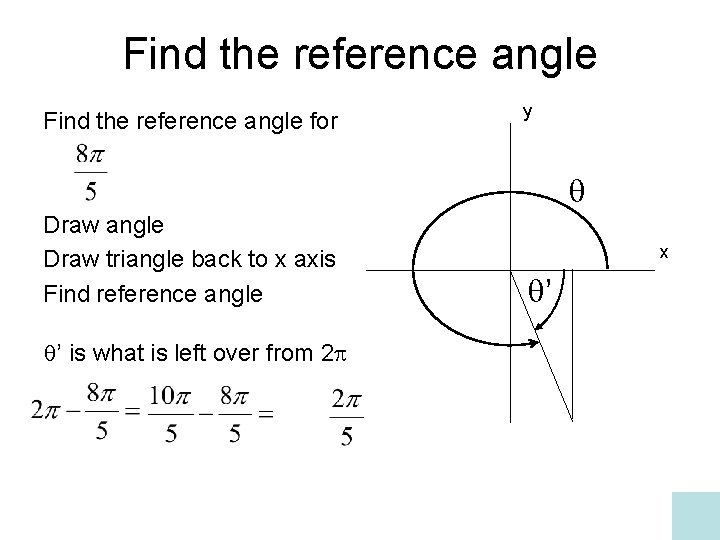
Note: 1. The reference angle of an angle is always non-negativeĢ. The reference angle of any angle always lies between 0 and π / 2. When the terminal side is in the fourth quadrant (angles from 270° to 360°), our reference angle is 360° minus our given angle. When the terminal side is in the third quadrant (angles from 180° to 270°), our reference angle is our given angle minus 180°. When the terminal side is in the second quadrant (angles from 90° to 180°), our reference angle is 180° minus our given angle. When the terminal side is in the first quadrant (angles from 0° to 90°), our reference angle is the same as our given angle. Since all the angles in the first quadrant are less than 90°.

Step 1: Enter the angle theta in the given input boxes.Please follow the below steps to find the reference angle: 'Cuemath's Reference Angle Calculator' is an online tool that helps to calculate the reference angle. Cuemath's online Reference Angle Calculator helps you to calculate the reference angle in a few seconds. A reference angle is formed by the terminal side and the x-axis and will therefore always be acute. ) where tan θ has no finite value.The reference angle is defined as the smallest possible angle made by the terminal side of the given angle with the x-axis. How to use reference angles to find the sine, cosine and tangent of non-acute angles To find the value of sine, cosine and tangent at non-acute angles (from 90 to 360), first draw the angle on the unit circle and find the reference angle. We see that there is a regular pattern that recurs every There are also "gaps" in the curve (at. Let's see what the graph of y = tan θ looks like. What it means is that there are many, many values of θ that will work in the equation tan θ = 0.3462. You will get a better idea of the periodic nature of trigonometric functions if you check out the chapter on Graphs of The Trigonometric Functions. Trigonometric functions are periodic, that is, their values re-occur over and over again.
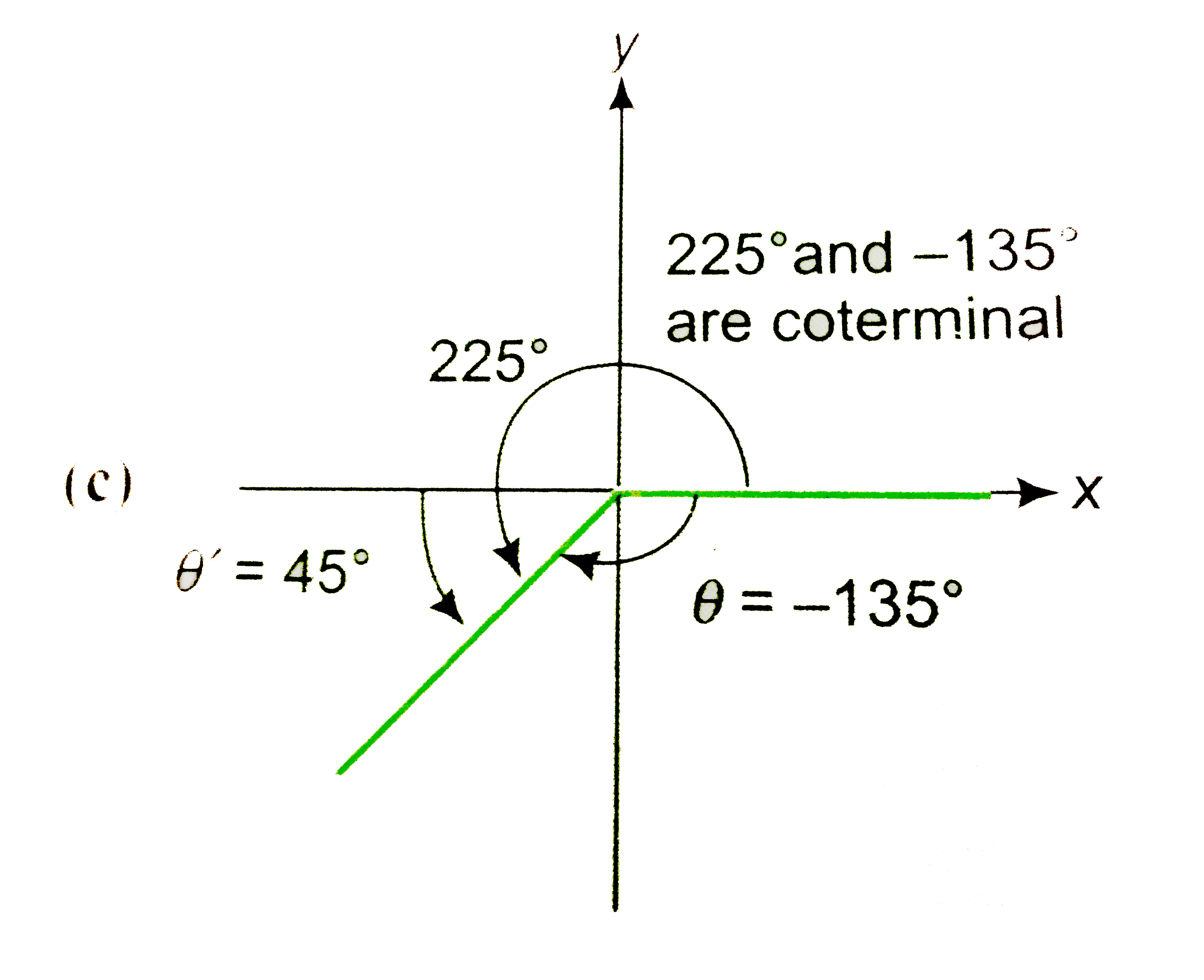
How many answers are there? Periodic Functions What's going on here? They all equal `0.3462`. And some negative angles also work: tan (-160.904 o) = 0.3462. Now we know this is correct because tan 19.096 o = 0.3462. Using our calculators, we found that θ = tan -10.3462 = 19.096 o. Trigonometric Functions of Any Angle Think About This.Įarlier, in the section Values of Trigonometric Functions, we were given the value of a trigonometric ratio and we needed to find the angle.


 0 kommentar(er)
0 kommentar(er)
